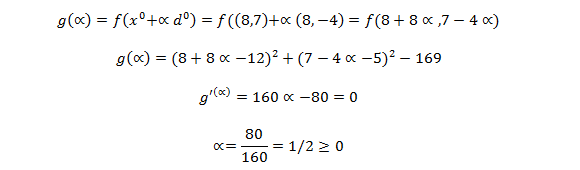Descenso del gradiente

El descenso del gradiente o gradiente descendiente es un algoritmo de optimización iterativo de primer orden que permite encontrar mínimos locales en una función diferenciable. La idea es tomar pasos de manera repetida en dirección contraria al gradiente. Esto se hace ya que esta dirección es la del descenso más empinado. Si se toman pasos con la misma dirección del gradiente, se encontrará el máximo local de la función; a esto se le conoce como el gradiente ascendente. Este algoritmo es utilizado para entrenar modelos de aprendizaje máquina y redes neuronales.

Historia

El gradiente descendiente se le atribuye generalmente a Augustin-Louis Cauchy, quien fue el primero en sugerirlo en 1847.^[1]​ Jacques Hadamard propuso un métodos similar en 1907.^[2]​ Haskell Curry fue el primero en estudiar las propiedades de convergencia para problemas de optimización no lineal en 1944.^[3]​ Desde entonces el método ha sido estudiado y utilizado a fondo.^[4]​

Requisitos

Para poder utilizar el algoritmo del gradiente descendiente la función de la cual se desea encontrar el mínimo local debe cumplir con lo siguiente:

1. La función debe ser diferenciable.
2. La función debe ser convexa:

Una función f es convexa si:

${\displaystyle f(\lambda x_{1} (1-\lambda )x_{2})<\lambda f(x_{1}) (1-\lambda )f(x_{2})}$

donde:

${\displaystyle \lambda \in \mathbb {R} }$,

${\displaystyle 0\leq \lambda \leq 1}$

Descripción

Idea General^[5]​

Para una función ${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ en un punto ${\displaystyle p=(x_{1},...,x_{n})}$ su gradiente se define como:

${\displaystyle \nabla f(p)={\begin{vmatrix}{\delta f \over \delta x_{1}}(p)\\\vdots \\{\delta f \over \delta x_{n}}(p)\end{vmatrix}}}$

El gradiente descendiente calcula iterativamente el siguiente punto utilizando el gradiente del punto actual. Este punto es escalado con una razón de aprendizaje ${\displaystyle \gamma \in \mathbb {R} ^{ }}$. Se tiene entonces que el gradiente descendiente utiliza la siguiente expresión:

${\displaystyle p_{n 1}=p_{n}-\gamma \nabla f(p_{n})}$

Algoritmo

El algoritmo del gradiente descendiente calcula iterativamente el siguiente punto usando el gradiente del punto en turno. Lo escala con la razón de aprendizaje y resta este resultado a la posición actual. Si la razón  de aprendizaje es muy pequeña, el algoritmo tarda en converger. Si la razón de aprendizaje es muy grande, el algoritmo puede no llegar a converger. El algoritmo del gradiente descendiente consta de los siguientes pasos:

1. Se elige un punto de salida de manera aleatoria,
2. Se calcula el gradiente en ese punto,
3. Se determina el siguiente punto de acuerdo con: ${\displaystyle p_{n 1}=p_{n}-\gamma \nabla f(p_{n})}$
4. Se detiene el algoritmo con una de las siguientes condiciones de paro:
   • Se llega a un número máximo de iteraciones predeterminado.
   • El tamaño del paso dado por el algoritmo es menor que un valor de tolerancia establecido.

Implementación en Python

Tipos de Gradiente Descendiente^[6]​

Con sondeo lineal

El descenso de gradiente con sondeo lineal guarda una notable similitud con el algoritmo del gradiente descendiente convencional. La distinción principal radica en que, en cada iteración, el valor del factor de aprendizaje 𝛾 se ajusta mediante la minimización de una nueva función unidimensional de la forma: ${\displaystyle g(\gamma )=f(p_{n}-\gamma \nabla f(p_{n}))}$, donde la única variable involucrada es ${\displaystyle \gamma }$. Esta característica permite aprovechar técnicas de optimización unidimensional, como la búsqueda de la sección dorada o la trisección, para determinar el valor óptimo de ${\displaystyle \gamma }$.

Batch

El gradiente descendiente batch suma el error para cada punto en un conjunto de entrenamiento, actualizando el modelo hasta que se hayan evaluado todos los ejemplos de entrenamiento disponibles. El proceso de batch provee mayor eficiencia a nivel computacional para conjuntos de datos grandes. Usualmente produce un error de gradiente estable y llega a converger.

Estocástico

El descenso de gradiente estocástico corre una época de entrenamiento para cada ejemplo en el conjunto de datos y actualiza los parámetros de cada ejemplo de entrenamiento uno a la vez. El gradiente descendiente estocástico realiza menos operaciones por actualización que el gradiente descendiente tradicional.

Mini-Batch

Combina elementos del gradiente descendiente batch y del gradiente descendiente estocástico. Divide el conjunto de entrenamiento en subconjuntos más pequeños y actualiza los parámetros de cada subconjunto.

Problemas del Gradiente Descendiente

Gradiente Explosivo

Este problema se presenta cuando el gradiente es demasiado grande, creando un modelo inestable. En este caso los pesos o ponderaciones asignados en el modelo crecerán demasiado. Una solución a este problema es utilizar una técnica para reducir la dimensionalidad y así reducir la complejidad del modelo.

Desvanecimiento del Gradiente

Durante el entrenamiento o ajuste de los parámetros de una red neuronal se utiliza la propagación hacia atrás con gradiente descendiente. Con cada iteración o paso el gradiente se hace más y más pequeño conforme la propagación hacia atrás llega a capas más profundas; el gradiente se desvanece. Esto trae como consecuencia que no se actualizan las conexiones de las capas más bajas o profundas y por lo tanto el entrenamiento no converge a una solución que sea de utilidad.

Referencias